In most martingale tests people fail to take into consideration the additional risk and only look at the reward. A single back-test or even a few to several back-tests will look great because it contains little or no drawdown. The user fails to realize the number of tests and the data sample size needed has gone up exponentially because of the variance this style of MM brings to the table. So, for this thought experiment, we will use pure math and work out every possible combination so that we don’t need to run hundreds of back-tests with bazillions of trades.
OK Let’s go. For simplicity’s sake, we will make it so that the only outcomes possible are a full loss or a full win. We will start with 4 units to risk over 3 trades with 8 possible total outcomes all worked out to provide an overall EV (Expected Value) of 3 trades. The system has a 50% chance of winning and wins 1.1x risk when it wins. Let’s define Risk of Ruin (RoR) as our chance of losing 75% of the 4 unit start account. Of course, we don’t normally make only 3 trades and risk such a high proportion of our risk capital but I will show later how the conclusions hold true when we add trades, increase our edge, reduce risk or reduce the martingale multiplier.
EV=(average) expected value
RoR=risk of ruin
Standard risk 0.43 unit on each trade NON-martingale:
| sum | ||||
|---|---|---|---|---|
| “L” | “L” | “L” | ||
| –1.29 | -0.43 | -0.43 | -0.43 | |
| “W” | “L” | “L” | ||
| –0.39 | 0.47 | -0.43 | -0.43 | |
| “L” | “W” | “L” | ||
| –0.39 | -0.43 | 0.47 | -0.43 | |
| “W” | “W” | “L” | ||
| 0.52 | 0.47 | 0.47 | -0.43 | |
| “L” | “L” | “W” | ||
| –0.39 | -0.43 | -0.43 | 0.47 | |
| “W” | “L” | “W” | ||
| 0.52 | 0.47 | -0.43 | 0.47 | |
| “L” | “W” | “W” | ||
| 0.52 | -0.43 | 0.47 | 0.47 | |
| “W” | “W” | “W” | ||
| 1.42 | 0.47 | 0.47 | 0.47 | |
| EV of 8 runs | 0.52 |
…
Martingale (2x) start risk 0.43 unit:
| sum | ||||
|---|---|---|---|---|
| “L” | “L” | “L” | ||
| –3.01 | -0.43 | -0.86 | -1.72 | |
| “W” | “L” | “L” | ||
| –0.82 | 0.47 | -0.43 | -0.86 | |
| “L” | “W” | “L” | ||
| 0.09 | -0.43 | 0.95 | -0.43 | |
| “W” | “W” | “L” | ||
| 0.52 | 0.47 | 0.47 | -0.43 | |
| “L” | “L” | “W” | ||
| 0.60 | -0.43 | -0.86 | 1.89 | |
| “W” | “L” | “W” | ||
| 0.99 | 0.47 | -0.43 | 0.95 | |
| “L” | “W” | “W” | ||
| 0.99 | -0.43 | 0.95 | 0.47 | |
| “W” | “W” | “W” | ||
| 1.42 | 0.47 | 0.47 | 0.47 | |
| EV of 8 runs | 0.77 |
Hey, the Martingale really is more profitable! Well, actually, we have taken on more risk so it’s not a fair comparison. Notice in the martingale we have 1 run that is -3 units. -3 units from our start balance of 4 is a ruin. 1 ruin in 8 is a 12.5% RoR. Let’s boost our risk on the NON-Martingale run so it too has a 12.5% Risk of Ruin.
…
Standard Risk 1 NON Martingale
| sum | ||||
|---|---|---|---|---|
| “L” | “L” | “L” | ||
| –3.00 | -1.00 | -1.00 | -1.00 | |
| “W” | “L” | “L” | ||
| –0.90 | 1.10 | -1.00 | -1.00 | |
| “L” | “W” | “L” | ||
| –0.90 | -1.00 | 1.10 | -1.00 | |
| “W” | “W” | “L” | ||
| 1.20 | 1.10 | 1.10 | -1.00 | |
| “L” | “L” | “W” | ||
| –0.90 | -1.00 | -1.00 | 1.10 | |
| “W” | “L” | “W” | ||
| 1.20 | 1.10 | -1.00 | 1.10 | |
| “L” | “W” | “W” | ||
| 1.20 | -1.00 | 1.10 | 1.10 | |
| “W” | “W” | “W” | ||
| 3.30 | 1.10 | 1.10 | 1.10 | |
| EV of 8 runs | 1.20 |
OK, there we have it, NON Martingale is miles ahead of Martingale in EV when we compare strategies with the same RoR. What if we reduce the Martingale Multiplier? A 1.5 multiplier and a 0.63 start size give us a 12.5% RoR so we can compare to the other runs…
…
Martingale (1.5x) start risk 0.63
| sum | ||||
|---|---|---|---|---|
| “L” | “L” | “L” | ||
| –2.99 | -0.63 | -0.95 | -1.42 | |
| “W” | “L” | “L” | ||
| –0.88 | 0.69 | -0.63 | -0.95 | |
| “L” | “W” | “L” | ||
| –0.22 | -0.63 | 1.04 | -0.63 | |
| “W” | “W” | “L” | ||
| 0.76 | 0.69 | 0.69 | -0.63 | |
| “L” | “L” | “W” | ||
| –0.02 | -0.63 | -0.95 | 1.56 | |
| “W” | “L” | “W” | ||
| 1.10 | 0.69 | -0.63 | 1.04 | |
| “L” | “W” | “W” | ||
| 1.10 | -0.63 | 1.04 | 0.69 | |
| “W” | “W” | “W” | ||
| 2.08 | 0.69 | 0.69 | 0.69 | |
| EV of 8 runs | 0.93 |
Still no dice for Marty. The best EV to RoR ratio is non-martingale. What if we increase the edge of the actual system? Let’s bring it from 1.1 to 1.5…
…
Martingale (1.5x) start risk 0.63
| sum | ||||
|---|---|---|---|---|
| “L” | “L” | “L” | ||
| –2.99 | -0.63 | -0.95 | -1.42 | |
| “W” | “L” | “L” | ||
| –0.63 | 0.95 | -0.63 | -0.95 | |
| “L” | “W” | “L” | ||
| 0.16 | -0.63 | 1.42 | -0.63 | |
| “W” | “W” | “L” | ||
| 1.26 | 0.95 | 0.95 | -0.63 | |
| “L” | “L” | “W” | ||
| 0.55 | -0.63 | -0.95 | 2.13 | |
| “W” | “L” | “W” | ||
| 1.73 | 0.95 | -0.63 | 1.42 | |
| “L” | “W” | “W” | ||
| 1.73 | -0.63 | 1.42 | 0.95 | |
| “W” | “W” | “W” | ||
| 2.84 | 0.95 | 0.95 | 0.95 | |
| EV of 8 runs | 4.65 |
…
Standard Risk 1 NON-Martingale
| sum | ||||
|---|---|---|---|---|
| “L” | “L” | “L” | ||
| –3.00 | -1.00 | -1.00 | -1.00 | |
| “W” | “L” | “L” | ||
| –0.50 | 1.50 | -1.00 | -1.00 | |
| “L” | “W” | “L” | ||
| –0.50 | -1.00 | 1.50 | -1.00 | |
| “W” | “W” | “L” | ||
| 2.00 | 1.50 | 1.50 | -1.00 | |
| “L” | “L” | “W” | ||
| –0.50 | -1.00 | -1.00 | 1.50 | |
| “W” | “L” | “W” | ||
| 2.00 | 1.50 | -1.00 | 1.50 | |
| “L” | “W” | “W” | ||
| 2.00 | -1.00 | 1.50 | 1.50 | |
| “W” | “W” | “W” | ||
| 4.50 | 1.50 | 1.50 | 1.50 | |
| EV of 8 runs | 6.00 |
Again the best EV comes from NON-Martingale. Can we do even better if we reduce risk slightly after a loss instead of increasing it? Let’s try a simple percentage risk of the current equity strategy. Apparently, we can achieve an RoR of 12.5% by risking 37% of current equity on each trade…
…
Percentage Risk 37% (NON Martingale)
| sum | first trade bal | 2nd bal | fin bal | ||||
|---|---|---|---|---|---|---|---|
| “L” | “L” | “L” | |||||
| –3.00 | -1.48 | 2.52 | -0.93 | 1.59 | -0.59 | 1.00 | |
| “W” | “L” | “L” | |||||
| –1.53 | 2.22 | 6.22 | -2.30 | 3.92 | -1.45 | 2.47 | |
| “L” | “W” | “L” | |||||
| –1.53 | -1.48 | 2.52 | 1.40 | 3.92 | -1.45 | 2.47 | |
| “W” | “W” | “L” | |||||
| 2.09 | 2.22 | 6.22 | 3.45 | 9.67 | -3.58 | 6.09 | |
| sum | “L” | first trade bal | “L” | 2nd bal | “W” | fin bal | |
| –1.53 | -1.48 | 2.52 | -0.93 | 1.59 | 0.88 | 2.47 | |
| “W” | “L” | “W” | |||||
| 2.09 | 2.22 | 6.22 | -2.30 | 3.92 | 2.17 | 6.09 | |
| “L” | “W” | “W” | |||||
| 2.09 | -1.48 | 2.52 | 1.40 | 3.92 | 2.17 | 6.09 | |
| “W” | “W” | “W” | |||||
| 11.04 | 2.22 | 6.22 | 3.45 | 9.67 | 5.37 | 15.04 | |
| EV of 8 runs | 9.73 |
OK, so the percent risk strategy has double the EV as a 1.5x Martingale strategy of the same RoR. OK well, what if we redefine RoR to be only -0.25(6.25% dd)? That should give us a more realistic risk compared to start capital for this small amount of runs.
…
Percentage Risk 2.1% (NON Martingale)
| sum | first trade bal | 2nd bal | fin bal | ||||
|---|---|---|---|---|---|---|---|
| “L” | “L” | “L” | |||||
| –0.25 | -0.08 | 3.92 | -0.08 | 3.83 | -0.08 | 3.75 | |
| “W” | “L” | “L” | |||||
| –0.05 | 0.13 | 4.13 | -0.09 | 4.04 | -0.08 | 3.95 | |
| “L” | “W” | “L” | |||||
| –0.05 | -0.08 | 3.92 | 0.12 | 4.04 | -0.08 | 3.95 | |
| “W” | “W” | “L” | |||||
| 0.17 | 0.13 | 4.13 | 0.13 | 4.26 | -0.09 | 4.17 | |
| sum | “L” | first trade bal | “L” | 2nd bal | “W” | fin bal | |
| –0.05 | -0.08 | 3.92 | -0.08 | 3.83 | 0.12 | 3.95 | |
| “W” | “L” | “W” | |||||
| 0.17 | 0.13 | 4.13 | -0.09 | 4.04 | 0.13 | 4.17 | |
| “L” | “W” | “W” | |||||
| 0.17 | -0.08 | 3.92 | 0.12 | 4.04 | 0.13 | 4.17 | |
| “W” | “W” | “W” | |||||
| 0.39 | 0.13 | 4.13 | 0.13 | 4.26 | 0.13 | 4.39 | |
| EV of 8 runs | 0.51 |
…
Martingale (1.5x) start risk 0.052
| sum | ||||
|---|---|---|---|---|
| “L” | “L” | “L” | ||
| –0.25 | -0.05 | -0.08 | -0.12 | |
| “W” | “L” | “L” | ||
| –0.05 | 0.08 | -0.05 | -0.08 | |
| “L” | “W” | “L” | ||
| 0.01 | -0.05 | 0.12 | -0.05 | |
| “W” | “W” | “L” | ||
| 0.10 | 0.08 | 0.08 | -0.05 | |
| “L” | “L” | “W” | ||
| 0.05 | -0.05 | -0.08 | 0.18 | |
| “W” | “L” | “W” | ||
| 0.14 | 0.08 | -0.05 | 0.12 | |
| “L” | “W” | “W” | ||
| 0.14 | -0.05 | 0.12 | 0.08 | |
| “W” | “W” | “W” | ||
| 0.23 | 0.08 | 0.08 | 0.08 | |
| EV of 8 runs | 0.38 |
…
Martingale loses again, you get the idea. We now know that if we want to increase profits by accepting more risk, we are always better off taking an additional risk by increasing our percent risk of equity on every single trade than we are switching to a Martingale of any kind.
The Illusion of Profitability
So, it’s not a death sentence though, what’s all this hype about how dangerous Martingale is? Well, something else we see is that Martingale has a disproportionate amount of winning runs vs losing runs. Adding to equity on each loser significantly increases the chance that any end trade in a sequence will end in a profitable run, but that doesn’t mean it’s got a better risk to reward, it does not, the EV of Martingale is always lower in the context of comparing methods of a similar risk of ruin. It does mean that effective balance draw-downs are made less likely usually delaying them but also increasing the damage. A much larger sample size will be required to converge on the true system performance of a given system where the edge is unknown. So much so that we can literally take a losing strategy and apply a large enough start account to a small enough starting lot and make it look profitable for some time. Let’s try it! Here’s a losing run…
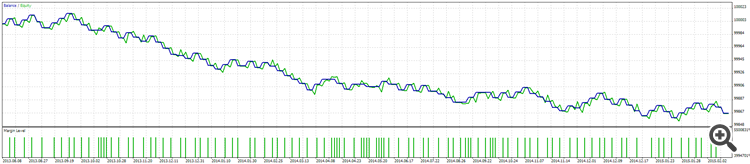
It’s very clear to the eye the performance of this strategy is poor and we have a negative EV here. But we can hide this with a simple Martingale MM…
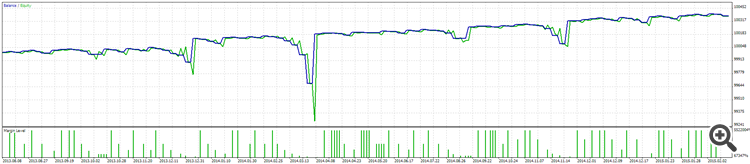
Like magic, we have created the illusion of profitability beyond the sample! But when losses do hit us they will be big. We now have (semi-) hidden enormous risk. Continuing to run the martingale with this losing strategy will result eventually in a larger loss than the non-martingale would lose in the same period. So, one danger is that poor performance can be masked by unscrupulous EA or signal providers… We need waaaay bigger sample size to properly judge any strategy in this case.
More Reasons to Quit being friends with Marty
But is it really that dangerous if we know we have an edge? Let’s compare two strategies with equal EV so we can compare the risk and also see how much the risk increases when we plan more trades. We will use the last Martingale table and compare it to a NON-martingale strategy of equal EV to compare risk in a fair manner.
…
Non Martingale is 1.57% risk
| sum | first trade bal | 2nd bal | fin bal | ||||
|---|---|---|---|---|---|---|---|
| “L” | “L” | “L” | |||||
| –0.19 | -0.06 | 3.94 | -0.06 | 3.88 | -0.06 | 3.81 | |
| “W” | “L” | “L” | |||||
| –0.03 | 0.09 | 4.09 | -0.06 | 4.03 | -0.06 | 3.97 | |
| “L” | “W” | “L” | |||||
| –0.03 | -0.06 | 3.94 | 0.09 | 4.03 | -0.06 | 3.97 | |
| “W” | “W” | “L” | |||||
| 0.12 | 0.09 | 4.09 | 0.10 | 4.19 | -0.07 | 4.12 | |
| sum | “L” | first trade bal | “L” | 2nd bal | “W” | fin bal | |
| –0.03 | -0.06 | 3.94 | -0.06 | 3.88 | 0.09 | 3.97 | |
| “W” | “L” | “W” | |||||
| 0.12 | 0.09 | 4.09 | -0.06 | 4.03 | 0.09 | 4.12 | |
| “L” | “W” | “W” | |||||
| 0.12 | -0.06 | 3.94 | 0.09 | 4.03 | 0.09 | 4.12 | |
| “W” | “W” | “W” | |||||
| 0.29 | 0.09 | 4.09 | 0.10 | 4.19 | 0.10 | 4.29 | |
| EV of 8 runs | 0.38 |
(Notice the EV is the same as our last Martingale run 0.38) So with a percent of equity strategy we are 12.5% chance of a 0.19 DD and a system of equal EV with the Martingale landed us at 12.5% chance of a 0.25 DD. What if we increase risk a little and drop the edge of our system from 1.5 back to 1.1…
…
Non Martingale 5% risk
| sum | first trade bal | 2nd bal | fin bal | ||||
|---|---|---|---|---|---|---|---|
| “L” | “L” | “L” | |||||
| –0.57 | -0.20 | 3.80 | -0.19 | 3.61 | -0.18 | 3.43 | |
| “W” | “L” | “L” | |||||
| –0.19 | 0.22 | 4.22 | -0.21 | 4.01 | -0.20 | 3.81 | |
| “L” | “W” | “L” | |||||
| –0.19 | -0.20 | 3.80 | 0.21 | 4.01 | -0.20 | 3.81 | |
| “W” | “W” | “L” | |||||
| 0.23 | 0.22 | 4.22 | 0.23 | 4.45 | -0.22 | 4.23 | |
| sum | “L” | first trade bal | “L” | 2nd bal | “W” | fin bal | |
| –0.19 | -0.20 | 3.80 | -0.19 | 3.61 | 0.20 | 3.81 | |
| “W” | “L” | “W” | |||||
| 0.23 | 0.22 | 4.22 | -0.21 | 4.01 | 0.22 | 4.23 | |
| “L” | “W” | “W” | |||||
| 0.23 | -0.20 | 3.80 | 0.21 | 4.01 | 0.22 | 4.23 | |
| “W” | “W” | “W” | |||||
| 0.70 | 0.22 | 4.22 | 0.23 | 4.45 | 0.24 | 4.70 | |
| EV of 8 runs | 0.24 |
…
Martingale (1.5x) 0.16 units start risk
| sum | ||||
|---|---|---|---|---|
| “L” | “L” | “L” | ||
| –0.76 | -0.16 | -0.24 | -0.36 | |
| “W” | “L” | “L” | ||
| –0.22 | 0.18 | -0.16 | -0.24 | |
| “L” | “W” | “L” | ||
| –0.06 | -0.16 | 0.26 | -0.16 | |
| “W” | “W” | “L” | ||
| 0.19 | 0.18 | 0.18 | -0.16 | |
| “L” | “L” | “W” | ||
| 0.00 | -0.16 | -0.24 | 0.40 | |
| “W” | “L” | “W” | ||
| 0.28 | 0.18 | -0.16 | 0.26 | |
| “L” | “W” | “W” | ||
| 0.28 | -0.16 | 0.26 | 0.18 | |
| “W” | “W” | “W” | ||
| 0.53 | 0.18 | 0.18 | 0.18 | |
| EV of 8 runs | 0.24 |
12.5% Chance of 0.57 DD vs Marty’s 12.5% chance of 0.76 DD. Significant but not deadly… yet… let’s add one more trade with exact same systems here as we already know Martingale always has the lower EV to RoR ratio, lets stay focused on the risk of trading Martingale over and over. Here are the two losing runs which now occur at a 6.25% frequency:
Non Martingale 5% risk – worse case
| sum | “L” | first trade bal | “L” | 2nd bal | “L” | fin bal | “L” | fin bal |
|---|---|---|---|---|---|---|---|---|
| –0.74 | -0.20 | 3.80 | -0.19 | 3.61 | -0.18 | 3.43 | -0.17 | 3.26 |
…
Martingale (1.5x) 0.16 start lot – worse case
| sum | “L” | “L” | “L” | “L” |
|---|---|---|---|---|
| –1.30 | -0.16 | -0.24 | -0.36 | -0.54 |
The risk of the Martingale is now nearly double that of the risk of the percent of equity strategy even though it has the same expectancy and we’re still using 1.5x for Marty instead of 2x! We can see the more trades we plan, the higher the risk jumps for Martingale in contrast to a percent of equity strategy even when we adjust them to have the same average expectancy. So, if for some reason the lower profitability to RoR ratio of any Martingale system isn’t a good enough reason to shy away from it (you don’t like money?) consider the additional risk of each additional planned trade in a Martingale strategy…